티스토리 뷰
서로소 집합
서로소(상호배타) 집합(Disjoint-sets)
- 서로소 또는 상호배타 집합이란 서로 중복 포함된 원소가 없는 집합, 교집합이 없는 집합이다.
- 집합에 속한 하나의 특정 멤버(대표)로 집합을 구분하며 이를 대표자(representative)라 한다.
상호배타 집합 연산
- Make-Set(x) : x 를 대표로 하는 집합을 만들어라!
# 초기설정
Make-Set(a) ~ Make-Set(f) : [0, 1, 2, 3, 4, 5, 6] 또는 [a, b, c, d, e, f] : 대표는 자기자신을 가리킨다.
- Find-Set(x) : x 가 속한 집합의 대표원소를 알아내라! 자기자신을 가리키는 원소(=대표원소)를 만날때 까지 찾는다.
- Union(x, y) : x가 속한 집합과 y가 속합 집합을 합쳐라! 대표 1개만 남기고!
Union(d, f) : f의 대표원소를 찾아서, 그 값을 d의 대표원소(c)로 바꾸자!

트리를 통한 상호배타집합 표현
하나의 집합을 하나의 트리로 표현한다.
자식 노드가 부모 노드를 가리키며, 루트 노드가 대표자가 된다.
대표는 자기자신을 대표로 가리키며 대표가 아니라면 대표원소를 가리킨다.
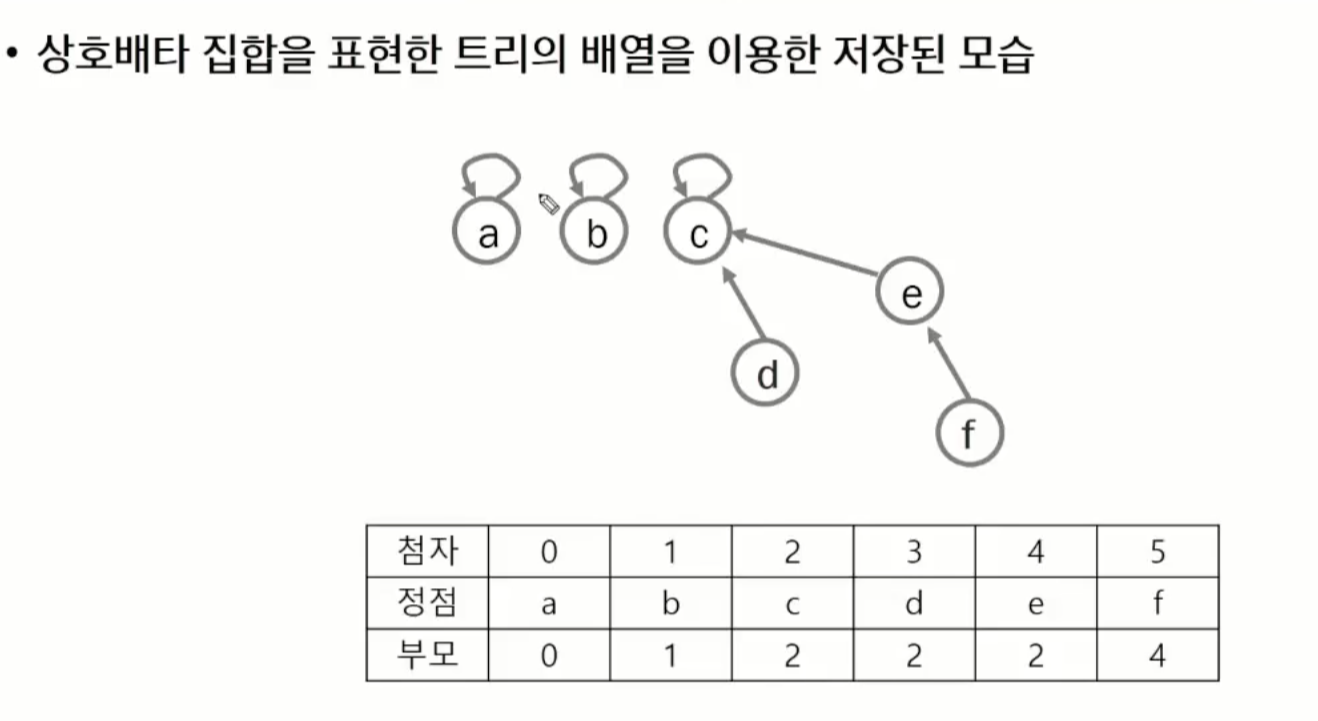



P = [1, 2, 3, 4, 5, 6]
P = [1, 2, 1, 4, 5, 6]
P = [2, 2, 1, 4, 5, 6]
P = [2, 2, 1, 4, 5, 5]
(추가) Rank를 사용하는 경우
각각의 대표원소의 Rank 를 비교하여, 더 rank 가 높은쪽을 가리키도록 한다.
만약 같다면 한 쪽의 rank 를 높인다.
MST 최소신장트리
그래프 최소비용문제
- 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리
- 두 정점 사이의 최소비용의 경로 찾기
신장 트리?
- n개의 정점으로 이루어진 무방향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리
최소 신장 트리 (Minimum Spanning Tree)
- 무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치의 합이 최소인 신장 트리
1. 프림 알고리즘 (Prim Algorithm)
- 하나의 정점에서 연결된 간선들 중 하나씩 선택하며 MST를 만들어가는 방식
- 1) 임의의 정점을 하나 선택해서 시작
- 2) 선택한 정점과 인접하는 정점들 중의 최소 비용의 간선이 존재하는 정점을 선택
- 3) 모든 정점이 선택될 때 까지 1), 2) 과정을 반복
- 서로소인 2개의 집합 정보를 유지한다.
- 트리 정점(tree vertices) : MST를 만들기 위해 선택된 정점들
- 비트리 정점(nontree vertices) : 선택되지 않은 정점들
# 방법 1
MST 초기화 [0, 0, 0, 0, 0, 0, 0] - 정점 6개인 경우
- 임의의 정점 선택하면 MST 를 1로 바꾼다.
- 이후 MST에 속한 정점 v 가 있을 때, MST에 속하지 않고 가중치가 최소인 인접 w를 선택
- 모든 정점이 MST에 포함되면 종료
필요없는 간선 쳐내기
선 중에서 가장 작은 것을 고르기
시작점 0, 나머지 무한대로 배치하고 임의의 시작점 정해 경로수를 업데이트해나간다.
기존값을 덮어씌운다. (갱신)
모든 경우의 수를 찾고나서 그림을 그리는 형태

2. 크루스칼 알고리즘 (Kruskal Algorithm)
- 1) 처음에 모든 간선을 가중치에 따라 오름차순으로 정렬한다.
- 2) 가중치가 가장 낮은 간선부터 선택하면서 트리를 증가시킨다.
- 사이클이 존재하면 건너뛰고 다음으로 가중치가 낮은 간선을 선택한다.
- 3) n-1개의 간선이 선택될 때 까지 2)를 반복한다.
사이클이 존재한다는 것은 => 선택한 두 노드의 대표원소가 동일하다는 것.
union을 통해 연결되어 있는 노드 중 가장 boss 노드를 루트로 연결한다.

'Algorithm' 카테고리의 다른 글
| 파이썬으로 순열과 조합 구현하기 (+중복순열, 중복조합) (3) | 2021.10.16 |
|---|---|
| 최단 경로와 다익스트라 알고리즘(Dijkstra Shortcut Path) (0) | 2021.10.16 |
| [SWEA] 2814. 최장 경로 D3 (0) | 2021.10.14 |
| [graph] BFS 기본 구현 (0) | 2021.10.13 |
| [graph] DFS 기본 구현 (0) | 2021.10.13 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 개발자커리
- 개발언어순위
- 클린코드
- ssafy6기
- SSAFY
- 한글무료폰트추천
- ssafy결과
- 폰트
- 상업용무료폰트
- ssafy합격후기
- 코딩도서
- 무료폰트추천
- 개발자도서추천
- 개발언어추천
- 싸피
- 맥과윈도우로깃허브
- 개발자책추천
- 개발자
- 임대차3법
- 개발자로드맵
- 깃허브계정2개
- 디즈니얼굴
- 브왈라
- 클린코더
- 싸피6기
- ssafy후기
- 폰트추천
- intj여자
- 깃허브계정
- 개발도서추천
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
글 보관함
