티스토리 뷰
Vertex 노드의 갯수와 Edge 간선의 갯수, 그리고 출발점과 연결점이 한 쌍으로 연결된 정보가 주어진다.
이때 인접행렬 또는 인접리스트로 정보를 받는다.
언제 인접행렬 / 인접리스트를 사용하나?
주어진 문제 상황에 따라 다르며 무엇이 더 좋고나쁘고, 어렵고 쉽고는 없다.
일반적으로는 노드 수가 1000개를 넘어가면 인접행렬보다는 인접리스트를 사용한다고 한다.
또한 유향그래프인지, 무향그래프인지 문제에 따라 다르므로 확인하자!
# 6 8
# 0 1 0 2 0 5 0 6 4 3 5 3 5 4 6 4
V, E = map(int, input().split())
edge = list(map(int, input().split()))인접행렬로 받기
노드 수 + 1만큼의 행렬, 0으로 구성된 이차원 리스트를 만든다.
엣지 수만큼 돌면서(이는 엣지리스트 / 2 만큼의 수) 출발점과 도착점을 각각 엣지의 짝수/홀수번째 인덱스로 찾고
앞서 만든 0으로 구성된 리스트에서 해당 행렬 자리를 1로 교체한다.
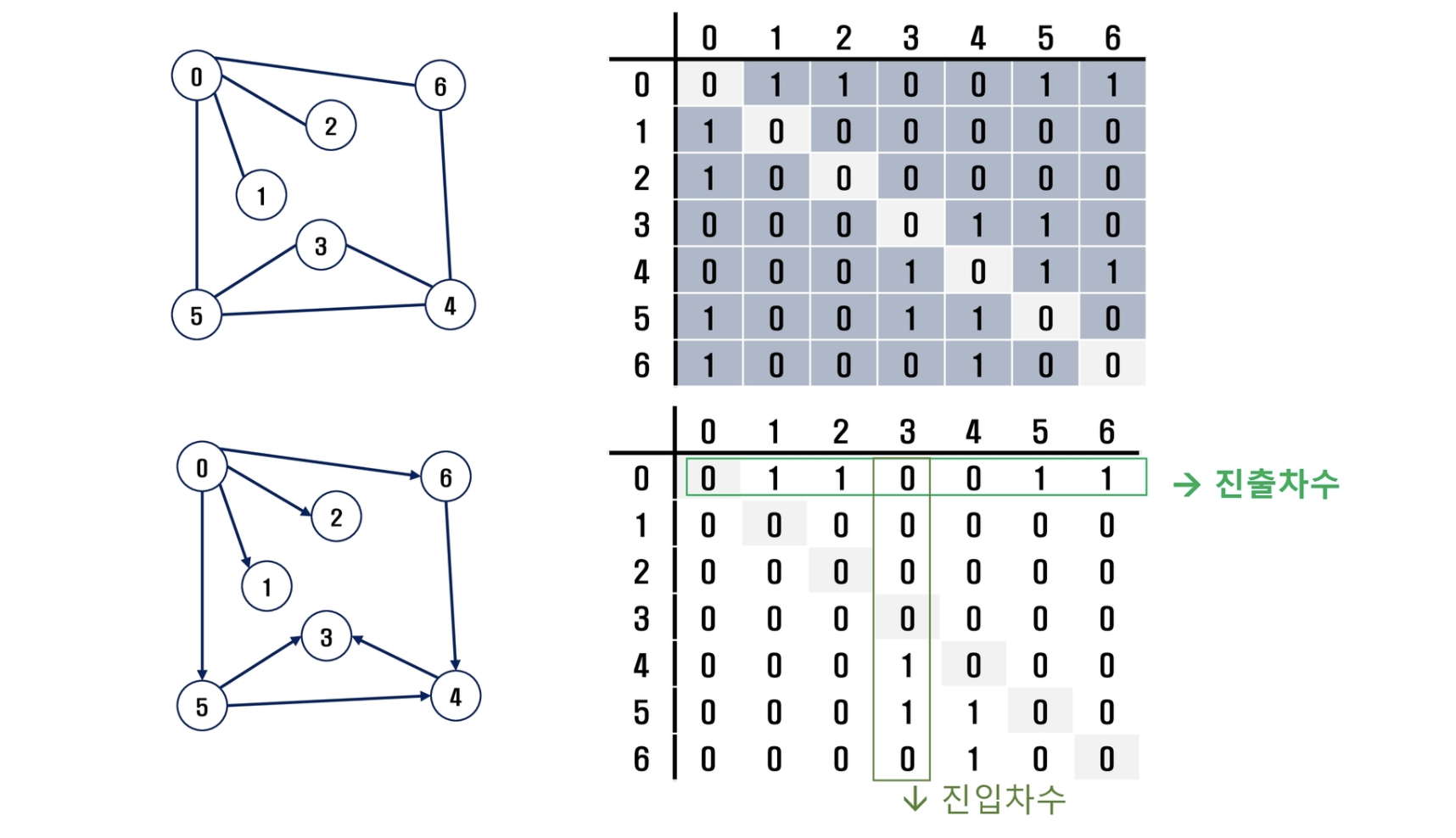
무향그래프일 경우 행과 열을 바꾸는 코드를 추가한다.
- 유향그래프
- 무향그래프
# 인접행렬(유향)
adjM = [[0]*(V+1) for _ in range(V+1)]
for i in range(E):
n1, n2 = edge[2*i], edge[2*i+1]
adjM[n1][n2] = 1
print(adjM)[
[0, 1, 1, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 0, 1, 0, 0]
]> i 번째 행의 합 = i 번째 열의 합 = Vi 의 차수
# 인접행렬(무향)
adjM = [[0]*(V+1) for _ in range(V+1)]
for i in range(E):
n1, n2 = edge[2*i], edge[2*i+1]
adjM[n1][n2] = 1
adjM[n2][n1] = 1
print(adjM)[
[0, 1, 1, 0, 0, 1, 1],
[1, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0],
[0, 0, 0, 1, 0, 1, 1],
[1, 0, 0, 1, 1, 0, 0],
[1, 0, 0, 0, 1, 0, 0]
]> 행 i의 합 = Vi의 진출 차수
> 열 i의 합 = Vi의 진입 차수
인접리스트로 받기
노드 수 + 1 크기의 이차원 리스트를 만든다.
이때, 각 행이 곧 노드가 되고 행 안의 데이터가 연결노드가 된다.
엣지 수만큼 돌면서 출발점과 도착점을 각각 엣지의 짝수/홀수번째 인덱스로 찾고
비어있는 리스트에 append한다.
무향그래프일 경우 행과 열을 바꾸어 추가한다.
- 유향그래프
- 무향그래프
# 인접리스트(유향)
adjL = [[] for _ in range(V+1)]
for i in range(E):
n1, n2 = edge[2*i], edge[2*i+1]
adjL[n1].append(n2)
print(adjL)[[1, 2, 5, 6], [], [], [], [3], [3, 4], [4]]# 인접리스트(무향)
adjL = [[] for _ in range(V+1)]
for i in range(E):
n1, n2 = edge[2*i], edge[2*i+1]
adjL[n1].append(n2)
adjL[n2].append(n1)
print(adjL)[[1, 2, 5, 6], [0], [0], [4, 5], [3, 5, 6], [0, 3, 4], [0, 4]]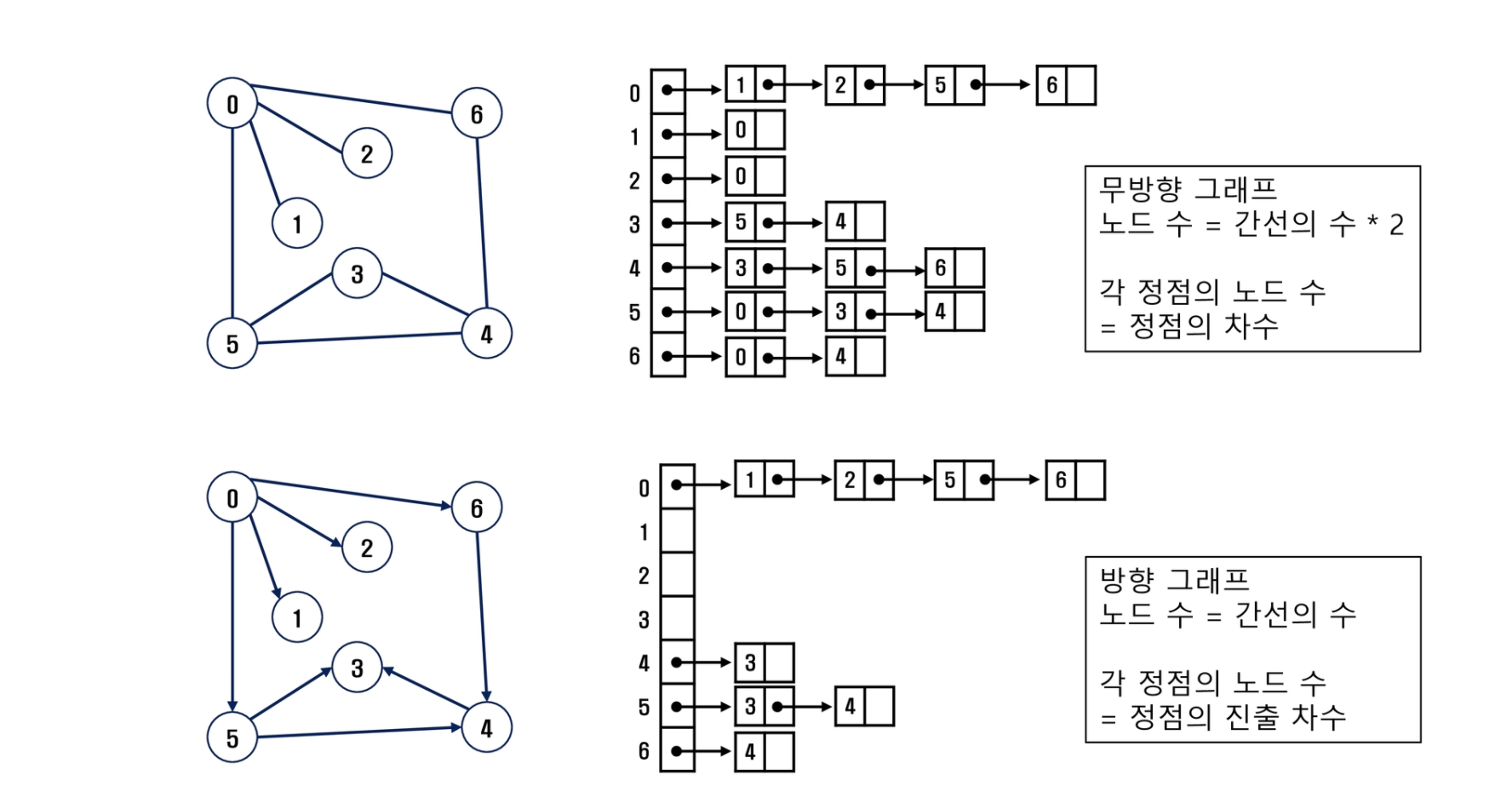
'Algorithm' 카테고리의 다른 글
| [graph] DFS 기본 구현 (0) | 2021.10.13 |
|---|---|
| [graph] 문제유형 3가지 : 완전탐색/MST/다익스트라 (0) | 2021.10.13 |
| [SWEA] 2105. [모의 SW 역량테스트] 디저트 카페 (0) | 2021.10.13 |
| [SWEA] 4012. [모의 SW 역량테스트] 요리사 (211012) (0) | 2021.10.12 |
| [1-2][DP] 거듭제곱 빠르게 구현하기 (0) | 2021.10.12 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 싸피6기
- ssafy6기
- SSAFY
- 개발자
- intj여자
- 개발도서추천
- 디즈니얼굴
- ssafy결과
- 폰트추천
- 깃허브계정
- 개발언어순위
- 개발자로드맵
- 싸피
- 무료폰트추천
- ssafy합격후기
- 폰트
- 개발자도서추천
- 브왈라
- ssafy후기
- 클린코더
- 깃허브계정2개
- 임대차3법
- 상업용무료폰트
- 스프링부트
- 개발언어추천
- 개발자커리
- 맥과윈도우로깃허브
- 개발자책추천
- 코딩도서
- 한글무료폰트추천
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
글 보관함
